This notebook shows how to compress a model using TensorFlow Compression.
In the example below, we compress the weights of an MNIST classifier to a much smaller size than their floating point representation, while retaining classification accuracy. This is done by a two step process, based on the paper Scalable Model Compression by Entropy Penalized Reparameterization:
This method is strictly concerned with compressed model size, not with computational complexity. It can be combined with a technique like model pruning to reduce size and complexity.
Example compression results on various models:
| Model (dataset) | Model size | Comp. ratio | Top-1 error comp. (uncomp.) |
|---|---|---|---|
| LeNet300-100 (MNIST) | 8.56 KB | 124x | 1.9% (1.6%) |
| LeNet5-Caffe (MNIST) | 2.84 KB | 606x | 1.0% (0.7%) |
| VGG-16 (CIFAR-10) | 101 KB | 590x | 10.0% (6.6%) |
| ResNet-20-4 (CIFAR-10) | 128 KB | 134x | 8.8% (5.0%) |
| ResNet-18 (ImageNet) | 1.97 MB | 24x | 30.0% (30.0%) |
| ResNet-50 (ImageNet) | 5.49 MB | 19x | 26.0% (25.0%) |
Applications include:
Install Tensorflow Compression via pip.# Installs the latest version of TFC compatible with the installed TF version.read MAJOR MINOR <<< "$(pip show tensorflow | perl -p -0777 -e 's/.*Version: (\d+)\.(\d+).*/\1 \2/sg')"pip install "tensorflow-compression<$MAJOR.$(($MINOR+1))"
Import library dependencies.
import matplotlib.pyplot as plt
import tensorflow as tf
import tensorflow_compression as tfc
import tensorflow_datasets as tfds2023-10-13 01:36:11.471586: E tensorflow/compiler/xla/stream_executor/cuda/cuda_dnn.cc:9342] Unable to register cuDNN factory: Attempting to register factory for plugin cuDNN when one has already been registered 2023-10-13 01:36:11.471633: E tensorflow/compiler/xla/stream_executor/cuda/cuda_fft.cc:609] Unable to register cuFFT factory: Attempting to register factory for plugin cuFFT when one has already been registered 2023-10-13 01:36:11.471669: E tensorflow/compiler/xla/stream_executor/cuda/cuda_blas.cc:1518] Unable to register cuBLAS factory: Attempting to register factory for plugin cuBLAS when one has already been registered
In order to effectively compress dense and convolutional layers, we need to define custom layer classes. These are analogous to the layers under tf.keras.layers, but we will subclass them later to effectively implement Entropy Penalized Reparameterization (EPR). For this purpose, we also add a copy constructor.
First, we define a standard dense layer:
class CustomDense(tf.keras.layers.Layer):
def __init__(self, filters, name="dense"):
super().__init__(name=name)
self.filters = filters
@classmethod
def copy(cls, other, **kwargs):
"""Returns an instantiated and built layer, initialized from `other`."""
self = cls(filters=other.filters, name=other.name, **kwargs)
self.build(None, other=other)
return self
def build(self, input_shape, other=None):
"""Instantiates weights, optionally initializing them from `other`."""
if other is None:
kernel_shape = (input_shape[-1], self.filters)
kernel = tf.keras.initializers.GlorotUniform()(shape=kernel_shape)
bias = tf.keras.initializers.Zeros()(shape=(self.filters,))
else:
kernel, bias = other.kernel, other.bias
self.kernel = tf.Variable(
tf.cast(kernel, self.variable_dtype), name="kernel")
self.bias = tf.Variable(
tf.cast(bias, self.variable_dtype), name="bias")
self.built = True
def call(self, inputs):
outputs = tf.linalg.matvec(self.kernel, inputs, transpose_a=True)
outputs = tf.nn.bias_add(outputs, self.bias)
return tf.nn.leaky_relu(outputs)And similarly, a 2D convolutional layer:
class CustomConv2D(tf.keras.layers.Layer):
def __init__(self, filters, kernel_size,
strides=1, padding="SAME", name="conv2d"):
super().__init__(name=name)
self.filters = filters
self.kernel_size = kernel_size
self.strides = strides
self.padding = padding
@classmethod
def copy(cls, other, **kwargs):
"""Returns an instantiated and built layer, initialized from `other`."""
self = cls(filters=other.filters, kernel_size=other.kernel_size,
strides=other.strides, padding=other.padding, name=other.name,
**kwargs)
self.build(None, other=other)
return self
def build(self, input_shape, other=None):
"""Instantiates weights, optionally initializing them from `other`."""
if other is None:
kernel_shape = 2 * (self.kernel_size,) + (input_shape[-1], self.filters)
kernel = tf.keras.initializers.GlorotUniform()(shape=kernel_shape)
bias = tf.keras.initializers.Zeros()(shape=(self.filters,))
else:
kernel, bias = other.kernel, other.bias
self.kernel = tf.Variable(
tf.cast(kernel, self.variable_dtype), name="kernel")
self.bias = tf.Variable(
tf.cast(bias, self.variable_dtype), name="bias")
self.built = True
def call(self, inputs):
outputs = tf.nn.convolution(
inputs, self.kernel, strides=self.strides, padding=self.padding)
outputs = tf.nn.bias_add(outputs, self.bias)
return tf.nn.leaky_relu(outputs)Before we continue with model compression, let’s check that we can successfully train a regular classifier.
Define the model architecture:
classifier = tf.keras.Sequential([
CustomConv2D(20, 5, strides=2, name="conv_1"),
CustomConv2D(50, 5, strides=2, name="conv_2"),
tf.keras.layers.Flatten(),
CustomDense(500, name="fc_1"),
CustomDense(10, name="fc_2"),
], name="classifier")2023-10-13 01:36:14.739153: W tensorflow/core/common_runtime/gpu/gpu_device.cc:2211] Cannot dlopen some GPU libraries. Please make sure the missing libraries mentioned above are installed properly if you would like to use GPU. Follow the guide at https://www.tensorflow.org/install/gpu for how to download and setup the required libraries for your platform. Skipping registering GPU devices…
Load the training data:
def normalize_img(image, label):
"""Normalizes images: `uint8` -> `float32`."""
return tf.cast(image, tf.float32) / 255., label
training_dataset, validation_dataset = tfds.load(
"mnist",
split=["train", "test"],
shuffle_files=True,
as_supervised=True,
with_info=False,
)
training_dataset = training_dataset.map(normalize_img)
validation_dataset = validation_dataset.map(normalize_img)Finally, train the model:
def train_model(model, training_data, validation_data, **kwargs):
model.compile(
optimizer=tf.keras.optimizers.Adam(learning_rate=1e-3),
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=[tf.keras.metrics.SparseCategoricalAccuracy()],
# Uncomment this to ease debugging:
# run_eagerly=True,
)
kwargs.setdefault("epochs", 5)
kwargs.setdefault("verbose", 1)
log = model.fit(
training_data.batch(128).prefetch(8),
validation_data=validation_data.batch(128).cache(),
validation_freq=1,
**kwargs,
)
return log.history["val_sparse_categorical_accuracy"][-1]
classifier_accuracy = train_model(
classifier, training_dataset, validation_dataset)
print(f"Accuracy: {classifier_accuracy:0.4f}")Epoch 1/5 469/469 [==============================] – 50s 104ms/step – loss: 0.2095 – sparse_categorical_accuracy: 0.9376 – val_loss: 0.0831 – val_sparse_categorical_accuracy: 0.9733 Epoch 2/5 469/469 [==============================] – 48s 103ms/step – loss: 0.0649 – sparse_categorical_accuracy: 0.9800 – val_loss: 0.0601 – val_sparse_categorical_accuracy: 0.9804 Epoch 3/5 469/469 [==============================] – 49s 103ms/step – loss: 0.0447 – sparse_categorical_accuracy: 0.9865 – val_loss: 0.0539 – val_sparse_categorical_accuracy: 0.9823 Epoch 4/5 469/469 [==============================] – 49s 104ms/step – loss: 0.0335 – sparse_categorical_accuracy: 0.9898 – val_loss: 0.0674 – val_sparse_categorical_accuracy: 0.9784 Epoch 5/5 469/469 [==============================] – 49s 104ms/step – loss: 0.0255 – sparse_categorical_accuracy: 0.9920 – val_loss: 0.0630 – val_sparse_categorical_accuracy: 0.9826 Accuracy: 0.9826
Success! The model trained fine, and reached an accuracy of over 98% on the validation set within 5 epochs.
Entropy Penalized Reparameterization (EPR) has two main ingredients:
Regularizer which implements this penalty.First, define the penalty.
The example below uses a code/probabilistic model implemented in the tfc.PowerLawEntropyModel class, inspired by the paper Optimizing the Communication-Accuracy Trade-off in Federated Learning with Rate-Distortion Theory. The penalty is defined as:
log(|�|+��),
where � is one element of the model parameter or its latent representation, and � is a small constant for numerical stability around values of 0.
_ = tf.linspace(-5., 5., 501)
plt.plot(_, tfc.PowerLawEntropyModel(0).penalty(_));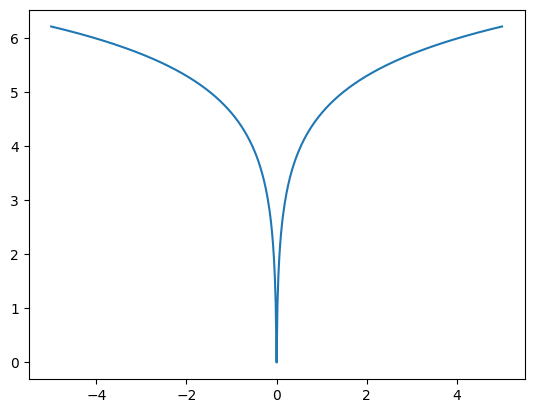
The penalty is effectively a regularization loss (sometimes called “weight loss”). The fact that it is concave with a cusp at zero encourages weight sparsity. The coding scheme applied for compressing the weights, an Elias gamma code, produces codes of length 1+⌊log2|�|⌋ bits for the magnitude of the element. That is, it is matched to the penalty, and applying the penalty thus minimizes the expected code length.
class PowerLawRegularizer(tf.keras.regularizers.Regularizer):
def __init__(self, lmbda):
super().__init__()
self.lmbda = lmbda
def __call__(self, variable):
em = tfc.PowerLawEntropyModel(coding_rank=variable.shape.rank)
return self.lmbda * em.penalty(variable)
# Normalizing the weight of the penalty by the number of model parameters is a
# good rule of thumb to produce comparable results across models.
regularizer = PowerLawRegularizer(lmbda=2./classifier.count_params())Second, define subclasses of CustomDense and CustomConv2D which have the following additional functionality:
@property, which perform quantization with straight-through gradients whenever the variables are accessed. This accurately reflects the computation that is carried out later in the compressed model.log_step variables, which represent the logarithm of the quantization step size. The coarser the quantization, the smaller the model size, but the lower the accuracy. The quantization step sizes are trainable for each model parameter, so that performing optimization on the penalized loss function will determine what quantization step size is best.The quantization step is defined as follows:
def quantize(latent, log_step):
step = tf.exp(log_step)
return tfc.round_st(latent / step) * stepWith that, we can define the dense layer:
class CompressibleDense(CustomDense):
def __init__(self, regularizer, *args, **kwargs):
super().__init__(*args, **kwargs)
self.regularizer = regularizer
def build(self, input_shape, other=None):
"""Instantiates weights, optionally initializing them from `other`."""
super().build(input_shape, other=other)
if other is not None and hasattr(other, "kernel_log_step"):
kernel_log_step = other.kernel_log_step
bias_log_step = other.bias_log_step
else:
kernel_log_step = bias_log_step = -4.
self.kernel_log_step = tf.Variable(
tf.cast(kernel_log_step, self.variable_dtype), name="kernel_log_step")
self.bias_log_step = tf.Variable(
tf.cast(bias_log_step, self.variable_dtype), name="bias_log_step")
self.add_loss(lambda: self.regularizer(
self.kernel_latent / tf.exp(self.kernel_log_step)))
self.add_loss(lambda: self.regularizer(
self.bias_latent / tf.exp(self.bias_log_step)))
@property
def kernel(self):
return quantize(self.kernel_latent, self.kernel_log_step)
@kernel.setter
def kernel(self, kernel):
self.kernel_latent = tf.Variable(kernel, name="kernel_latent")
@property
def bias(self):
return quantize(self.bias_latent, self.bias_log_step)
@bias.setter
def bias(self, bias):
self.bias_latent = tf.Variable(bias, name="bias_latent")The convolutional layer is analogous. In addition, the convolution kernel is stored as its real-valued discrete Fourier transform (RDFT) whenever the kernel is set, and the transform is inverted whenever the kernel is used. Since the different frequency components of the kernel tend to be more or less compressible, each of them gets its own quantization step size assigned.
Define the Fourier transform and its inverse as follows:
def to_rdft(kernel, kernel_size):
# The kernel has shape (H, W, I, O) -> transpose to take DFT over last two
# dimensions.
kernel = tf.transpose(kernel, (2, 3, 0, 1))
# The RDFT has type complex64 and shape (I, O, FH, FW).
kernel_rdft = tf.signal.rfft2d(kernel)
# Map real and imaginary parts into regular floats. The result is float32
# and has shape (I, O, FH, FW, 2).
kernel_rdft = tf.stack(
[tf.math.real(kernel_rdft), tf.math.imag(kernel_rdft)], axis=-1)
# Divide by kernel size to make the DFT orthonormal (length-preserving).
return kernel_rdft / kernel_size
def from_rdft(kernel_rdft, kernel_size):
# Undoes the transformations in to_rdft.
kernel_rdft *= kernel_size
kernel_rdft = tf.dtypes.complex(*tf.unstack(kernel_rdft, axis=-1))
kernel = tf.signal.irfft2d(kernel_rdft, fft_length=2 * (kernel_size,))
return tf.transpose(kernel, (2, 3, 0, 1))With that, define the convolutional layer as:
class CompressibleConv2D(CustomConv2D):
def __init__(self, regularizer, *args, **kwargs):
super().__init__(*args, **kwargs)
self.regularizer = regularizer
def build(self, input_shape, other=None):
"""Instantiates weights, optionally initializing them from `other`."""
super().build(input_shape, other=other)
if other is not None and hasattr(other, "kernel_log_step"):
kernel_log_step = other.kernel_log_step
bias_log_step = other.bias_log_step
else:
kernel_log_step = tf.fill(self.kernel_latent.shape[2:], -4.)
bias_log_step = -4.
self.kernel_log_step = tf.Variable(
tf.cast(kernel_log_step, self.variable_dtype), name="kernel_log_step")
self.bias_log_step = tf.Variable(
tf.cast(bias_log_step, self.variable_dtype), name="bias_log_step")
self.add_loss(lambda: self.regularizer(
self.kernel_latent / tf.exp(self.kernel_log_step)))
self.add_loss(lambda: self.regularizer(
self.bias_latent / tf.exp(self.bias_log_step)))
@property
def kernel(self):
kernel_rdft = quantize(self.kernel_latent, self.kernel_log_step)
return from_rdft(kernel_rdft, self.kernel_size)
@kernel.setter
def kernel(self, kernel):
kernel_rdft = to_rdft(kernel, self.kernel_size)
self.kernel_latent = tf.Variable(kernel_rdft, name="kernel_latent")
@property
def bias(self):
return quantize(self.bias_latent, self.bias_log_step)
@bias.setter
def bias(self, bias):
self.bias_latent = tf.Variable(bias, name="bias_latent")Define a classifier model with the same architecture as above, but using these modified layers:
def make_mnist_classifier(regularizer):
return tf.keras.Sequential([
CompressibleConv2D(regularizer, 20, 5, strides=2, name="conv_1"),
CompressibleConv2D(regularizer, 50, 5, strides=2, name="conv_2"),
tf.keras.layers.Flatten(),
CompressibleDense(regularizer, 500, name="fc_1"),
CompressibleDense(regularizer, 10, name="fc_2"),
], name="classifier")
compressible_classifier = make_mnist_classifier(regularizer)And train the model:
penalized_accuracy = train_model(
compressible_classifier, training_dataset, validation_dataset)
print(f"Accuracy: {penalized_accuracy:0.4f}")Epoch 1/5 469/469 [==============================] – 55s 112ms/step – loss: 3.8085 – sparse_categorical_accuracy: 0.9309 – val_loss: 2.1911 – val_sparse_categorical_accuracy: 0.9736 Epoch 2/5 469/469 [==============================] – 52s 112ms/step – loss: 1.6701 – sparse_categorical_accuracy: 0.9774 – val_loss: 1.3080 – val_sparse_categorical_accuracy: 0.9798 Epoch 3/5 469/469 [==============================] – 53s 112ms/step – loss: 1.0760 – sparse_categorical_accuracy: 0.9842 – val_loss: 0.9563 – val_sparse_categorical_accuracy: 0.9831 Epoch 4/5 469/469 [==============================] – 53s 112ms/step – loss: 0.8019 – sparse_categorical_accuracy: 0.9869 – val_loss: 0.7472 – val_sparse_categorical_accuracy: 0.9844 Epoch 5/5 469/469 [==============================] – 53s 112ms/step – loss: 0.6659 – sparse_categorical_accuracy: 0.9882 – val_loss: 0.6986 – val_sparse_categorical_accuracy: 0.9859 Accuracy: 0.9859
The compressible model has reached a similar accuracy as the plain classifier.
However, the model is not actually compressed yet. To do this, we define another set of subclasses which store the kernels and biases in their compressed form – as a sequence of bits.
Source: Tensorflow
You need to login in order to like this post: click here
YOU MIGHT ALSO LIKE