Gradient Descent trong trí tuệ nhân tạo

Khi xử lý các bài toán trong trí tuệ nhân tạo, vấn đề luôn phải giải quyết đó là tối ưu hàm mục tiêu hay hàm loss để tìm được bộ tham số mô hình tốt nhất. Một trong những thuật toán cơ bản nhất thường được giới thiệu đó chính là gradient descent.

I Ôn tập lại kiến thức về đạo hàm

Đạo hàm có thể tách nghĩa thành 2 phần, đạo theo tiếng hán là đường đi, hàm là hàm số ám chỉ sự biến đổi của hàm. Khi gộp lại ta có thể hiểu đơn giản là sự biến đổi của đường biểu diễn của hàm số, ngắn gọn là độ dốc của hàm số.

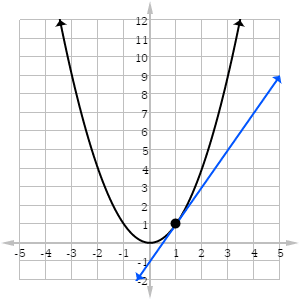
Một hàm số cơ bản từng học như f(x) = x^2 thì có đạo hàm là f'(x) = 2 * x.

Từ độ thị thì ta có thể thấy:

• Tại x = 1, f'(x) = 2 và tại x = 2, f'(x) = 4. Ta thấy đường màu xanh có thể coi là biểu thị độ dốc của hàm f(x) tại vị trí x = 2. Vì f'(x=2) > f'(x=1) nên ta có thể nói độ dốc của hàm f(x) tại điểm x = 2 “dốc” hơn so với tại điểm x = 1. Ta có thể vẽ lại đường biểu diễn để hiểu rõ hơn. Qua những điểm trên, có thể hiểu một cách trực quan về đạo hàm.
• Ta thấy tại x = -1, đạo hàm bằng -2. Đồ thị các điểm quanh điểm đó đang giảm, tiến gần tới điểm x = 0 là điểm hàm số f(x) có giá trị cực tiểu. Mặt khác tại điểm x = 1, đạo hàm bằng 2. Đồ thị các điểm quanh điể đó đang tăng, dịch xa so với điểm x =0. Qua đó, ta có thể kết luận:
  • Tại các điểm có đạo hàm âm, đồ thị có xu hướng giảm, các điểm có đạo hàm dương, đồ thị có xu hướng tăng.
  • Ta thấy khi xi = -1, nếu ta cập nhật giá trị x’ = x – xi * s = x – (-1)*s trong đó s là hằng số dương cập nhật giá trị thì x tiến gần tới điểm x =0 hơn. khi xi = 1, cập nhật giá trị x’ = x – xi * s = x – 1 * s thì x tiến gần tới điểm x = 0 nơi mà hàm số đạt cực tiểu.

Dựa trên các đặc điểm này đã tạo nên thuật toán gradient descent áp dụng vào quá trình tối ưu hàm loss khi huấn luyện model.

II Gradient Descent

Thuật toán Gradient Descent là một thuật toán tìm giá trị nhỏ nhất của 1 hàm số dựa trên đạo hàm.

Các bước của thuật toán:

• Bước 1: Khởi tạo giá trị tham số của model tùy ý. x = xi
• Bước 2: Tính giá trị đạo hàm của hàm tối ưu f(x) ở điểm xi và cập nhật tham số x. x = x – learning_rate * f'(xi). Trong đó learning rate là hằng số không âm biểu thị cho tốc độ cập nhật tham số, hay được gọi là tốc độ học.
• Bước 3: Tính lại giá trị của hàm tối ưu tại điểm mới. Nếu f(x) đủ nhỏ thì dừng lại, nếu không tiếp tục quay lại bước 2.

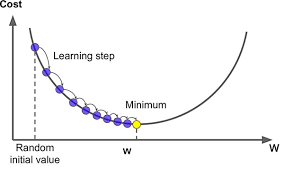
Hình trên mình họa quá trình tìm ra tham số x tối ưu cho 1 hàm f(x) = x^2 cơ bản.

Qua đây ta có thể có 1 cái nhìn tổng quan về cách tìm là tối ưu 1 mô hình học máy cơ bản.

1 số vấn đề cần quan tâm đặt ra khi sử dụng thuật toán trên:

a, Việc chọn tham số learning rate

Viêc chọn tham số trên anh hưởng rất nhiều đến viêc có tìm được tham số tối ưu không. Ảnh dưới đây thể hiện khái quát vấn đề của tham số:

• Nếu learning rate quá nhỏ, mỗi lần cập nhật hàm số giảm rất chậm, phải mất rất nhiều thời gian để có thể đến được điểm tối ưu.
• Nếu learning rate quá lớn, mỗi lần cập nhật quá lớn khiến cho rất lâu mới có thể hội tụ tại điểm tối ưu, thường được gọi là hiện tượng overshoot.

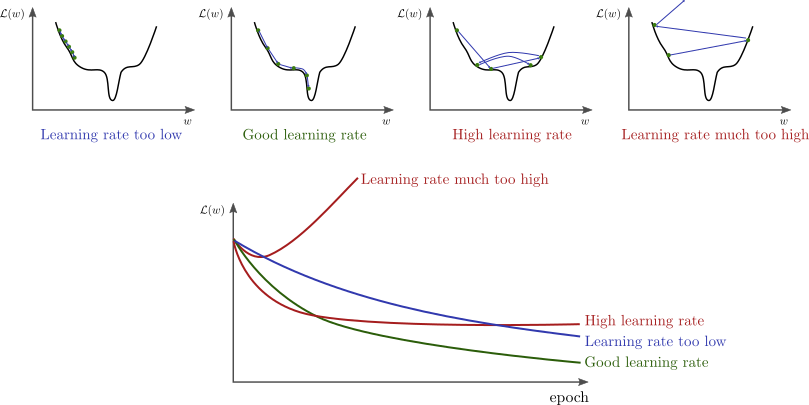
Cách khắc phục:

• Điều tra tham khảo các tham số learning rate của các model đã được nghiên cứu trước để chọn sao cho phù hợp
• Tuning hyper parametter
• Visualize hàm số để hiểu về hàm số cần tối ưu

b, Nếu hàm số có nhiều điểm cực tiểu

Nếu learning rate không đủ lớn rất có thể điểm cực tiểu chúng ta tìm thấy không phải điểm cực tiểu tối ưu nhất như hình dưới:

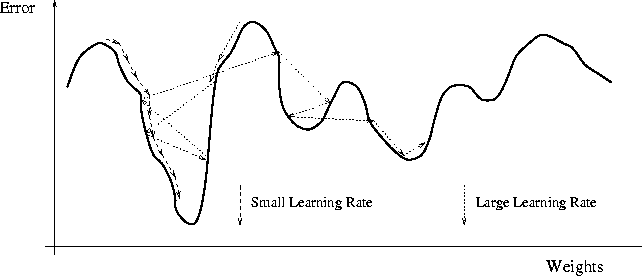
Cách khắc phục: sử dụng thuật toán momentum.

c, Việc tính toán đạo hàm của hàm nhiều biến

Đối với việc tính đạo hàm của các hàm nhiều biến thường rất khó khăn, khá phức tạp và dễ mắc lỗi, nên có thể dẫn tới việc tính sai đạo hàm làm quá trì tìm tham số tối ưu bị sai lệch.

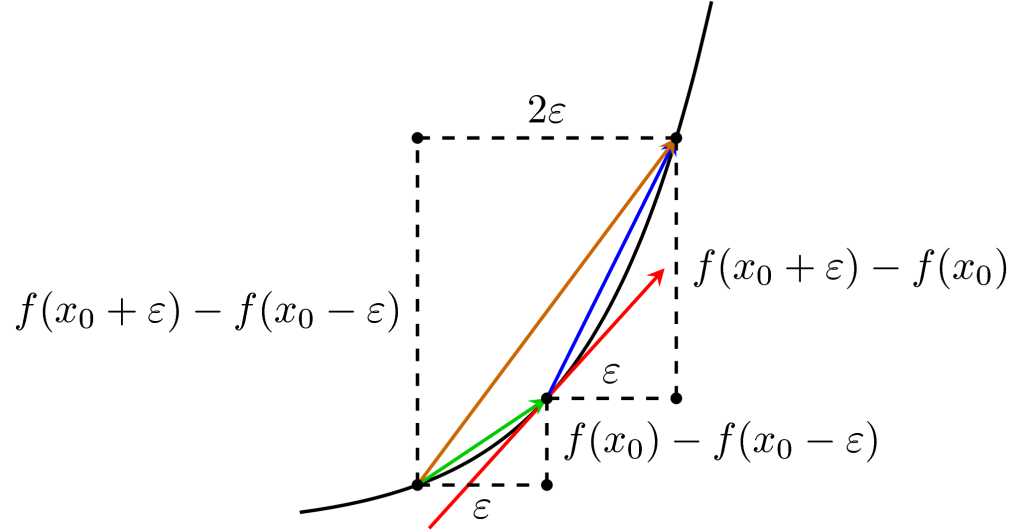
Cách khắc phục: sử dụng các công thức tính xấp sỉ dạo hàm để kiểm tra xem việc tính đạo hàm có chính xác.

Qua bài viết cho mọi người 1 cái nhìn tổng quát về ý tưởng huấn luyện 1 model AI như thế nào và các tối ưu các tham số của mô hình ra sao. Ngoài ra còn rất nhiều các tối ưu ngoài Gradient Descent như Adam, Adamax, RMSProp, … khuyến khích tìm hiểu sâu hơn. Cảm ơn vì đã đọc bài viết.

III Tham Khảo

[1] https://machinelearningcoban.com/2017/01/12/gradientdescent/

[2] http://www.bdhammel.com/learning-rates/

You need to login in order to like this post: click here